Chartanalysen Square - Fibonacci

Fibonacci-Zahlen

Leonardo de Pisa, besser bekannt als Fibonacci, gilt als bedeutender Mathematiker im Mittelalter. Seine Fibonacci-Zahlen bzw. die Zahlenreihe (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ...) ist wohl sein berühmtestes Erbe und unter anderem Grundlage für eine Vielzahl von Werkzeugen in der Charttechnik.

Die Zahlenreihe beginnt mit 0 und 1 und jede weitere Zahl ergibt sich aus der Summe ihrer beiden Vorgänger.

Die Fibonacci Folge in der Natur

Ein sehr besonderer Aspekt der Fibonacci Zahlenreihe ist deren vielfältiges Vorkommen in der Natur. Bei Blumen, Muscheln und Populationsberechnungen von Tieren entdeckt man immer wieder den Zusammenhang zu den Fibonacci-Zahlen. Fibonaccis Aufzeichnungen über die modellhafte Kaninchenpopulation stellen die Verbindung zur Natur sehr anschaulich dar. Fibonacci geht von den folgenden vier Voraussetzungen aus:

1. Ausgangslage ist ein Kaninchenpaar (geschlechtsreif)
2. Neugeborene Pärchen werden ab dem 2. Monat geschlechtsreif
3. Jeden Monat bringt ein Kaninchenpaar (geschlechtsreif) ein neues Kaninchenpaar auf die Welt
4. Da es sich um eine Modellsituation handelt, wird davon ausgegangen, dass kein Kaninchen das "System" verläßt und Keines von Außen hinzu kommt

Nach einem Monat bekommt das erste Kaninchenpaar direkt Nachwuchs. Für die zukünftigen Monate gilt, dass jedes geschlechtsreife Kaninchenpaar Nachwuchs bekommt, was bedeutet, dass jeden Monat soviel neugeborene Paare zu Welt kommen, wie Paare im vorletzten Monat gelebt haben. Die Verzögerung um einen Monat resultiert aus der fehlenden Geschlechtsreife der Neugeborenen.

Für das erste Jahr der Kaninchenpopulation ergibt dies auf Monatsbasis folgende Fortpflanzungssequenz für das erste Jahr: 1 (Jan.), 2 (Feb.), 3 (März), 5 (Apr.), 8 (Mai), 13 (Juni), 21 (Juli), 34 (Aug.), 55 (Sep.), 89 (Okt.), 144 (Nov.), 233 (Dez.) (1+2=3, 2+3=5, 3+5=8, etc.). Theoretisch kann die Population unendlich groß werden, wenn man den Kaninchen Unsterblichkeit unterstellt.

Die Fibonacci Folge in der Charttechnik

In der Chartanalyse dienen verschiedene Werkzeuge, deren Grundlage auf den Fibonacci Zahlen basieren, als Hilfsmittel zur Prognose von Kursbewegungen.

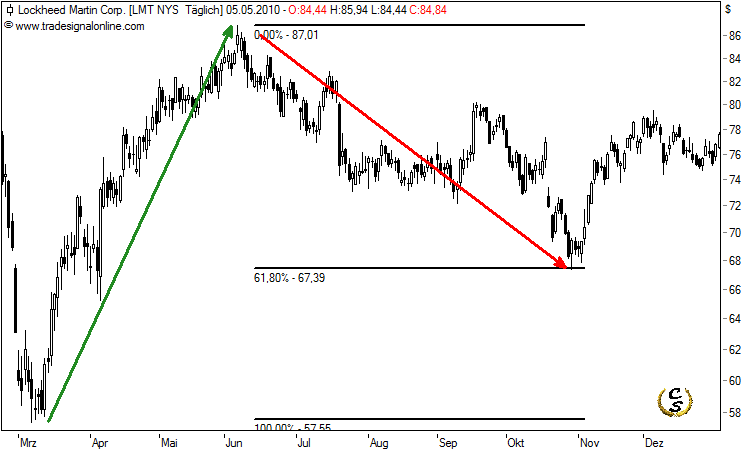
Besonders häufig werden die Fibonacci Retracements in der Praxis angewendet. In einem intakten Aufwärtstrend dient das 50% und das 61,8% Retracement als Ziel einer Korrektur. Erreicht der Kurs diese Niveaus gilt es aus charttechnischer Sicht als sehr wahrscheinlich, dass dort die Kurse einen Boden ausbilden und erneut in Richtung des vorherrschenden Trends ansteigen. Gleiches gilt für Erholungsbewegungen in Bärenmärkten.

Diese Retracement-Niveaus resultieren indirekt aus der Fibonacci-Zahlenreihe. Wird eine beliebige Zahl der Fibonacci-Reihe durch die Nächsthöhere dividiert, erhält man als Ergebnis immer einen Wert Nahe ~0,618 (z.B. 55 : 89 = 0,61797)! Bei Division durch die übernächste Zahl aus der Reihe ergibt sich immer ein Wert Nahe ~0,382 (z.B. 55 : 144 = 0,38194)! Je höher die verwendeten Fibonacci-Zahlen, desto genauer nähern sich die Ergebnisse diesen Grenzwerten an.

Beispiele von Fibonacci Retracements